Defining a Custom Material and Saving Output

We will define a redshift material for raytracing, and export the ray traced quantities to a .npy file.

using Krang

Materials should be functors (i.e. types with callable objects). Our material will ray trace the redshifts associated with a zero angular momentum observer (ZAMO) on a cone for a given sub-image. If the cone is self obscuring, then only the redshift on the side that is closest to the observer will be ray traced.

Defining the material

All materials must be subtypes of AbstractMaterial.

struct ZAMORedshifts{T} <: Krang.AbstractMaterial
    subimgs::Tuple{Int}
    rmin::T
    rmax::T
end

Define the function for the material. This functor will take in a pixel and a geometry and return the redshift associated with a given sub image. You must include the relevant physics in the functor definition. Here we will include redshift effects associated with a zero angular momentum observer (ZAMO).

function (m::ZAMORedshifts)(
    pix::Krang.AbstractPixel{T},
    intersection::Krang.Intersection,
) where {T}
    (; rs, θs, νr, νθ) = intersection
    α, β = Krang.screen_coordinate(pix)

    ηtemp = η(metric, α, β, θo)
    λtemp = λ(metric, α, θo)
    curr_p_bl_d = p_bl_d(metric, rs, θs, ηtemp, λtemp, νr, νθ)

    curr_p_bl_u = metric_uu(metric, rs, θs) * curr_p_bl_d
    p_zamo_u = jac_zamo_u_bl_d(metric, rs, θs) * curr_p_bl_u
    redshift = inv(p_zamo_u[1])

    return max(redshift, eps(T))
end

Ray tracing the material

We will use a $0.94$ spin Kerr black hole viewed by an asymptotic observer at an inclination angle of $\theta o={17}^{\circ }$. The emission to be ray traced is

metric = Krang.Kerr(0.99);
θo = 17 * π / 180;
ρmax = 15.0;
rmin = Krang.horizon(metric); # minimum radius to truncate cone
rmax = 10.0; # maximum radius to truncate cone
n = 1; # sub-image to ray trace

Let's create a camera with a resolution of 400x400 pixels and our mesh.

camera = Krang.IntensityCamera(metric, θo, -ρmax, ρmax, -ρmax, ρmax, 400);
mesh = Krang.Mesh(Krang.ConeGeometry((75 * π / 180)), ZAMORedshifts((n,), rmin, rmax))
scene = Krang.Scene((mesh,))

(Krang.Mesh{Krang.ConeGeometry{Float64, Nothing}, Main.var"Main".ZAMORedshifts{Float64}}(Krang.ConeGeometry{Float64, Nothing}(1.3089969389957472, nothing), Main.var"Main".ZAMORedshifts{Float64}((1,), 1.141067359796659, 10.0)),)

Finally, we will render the scene with the camera and plot the redshifts.

redshifts = render(camera, scene)

400×400 Matrix{Float64}:
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 ⋮                        ⋮              ⋱            ⋮                   
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0

Plotting the redshifts

import CairoMakie as CMk

theme = CMk.Theme(
    Axis = (
        xticksvisible = false,
        xticklabelsvisible = false,
        yticksvisible = false,
        yticklabelsvisible = false,
    ),
)

CMk.set_theme!(CMk.merge!(theme, CMk.theme_latexfonts()))

fig = CMk.Figure(resolution = (700, 700));
ax = CMk.Axis(fig[1, 1], title = "Redshifts", titlesize = 20, aspect = 1)
hm = CMk.heatmap!(ax, redshifts, colormap = :afmhot)
CMk.Colorbar(fig[1, 2], hm, label = "Redshifts", labelsize = 20)
CMk.save("redshifts.png", fig)

┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/6zcxH/src/scenes.jl:264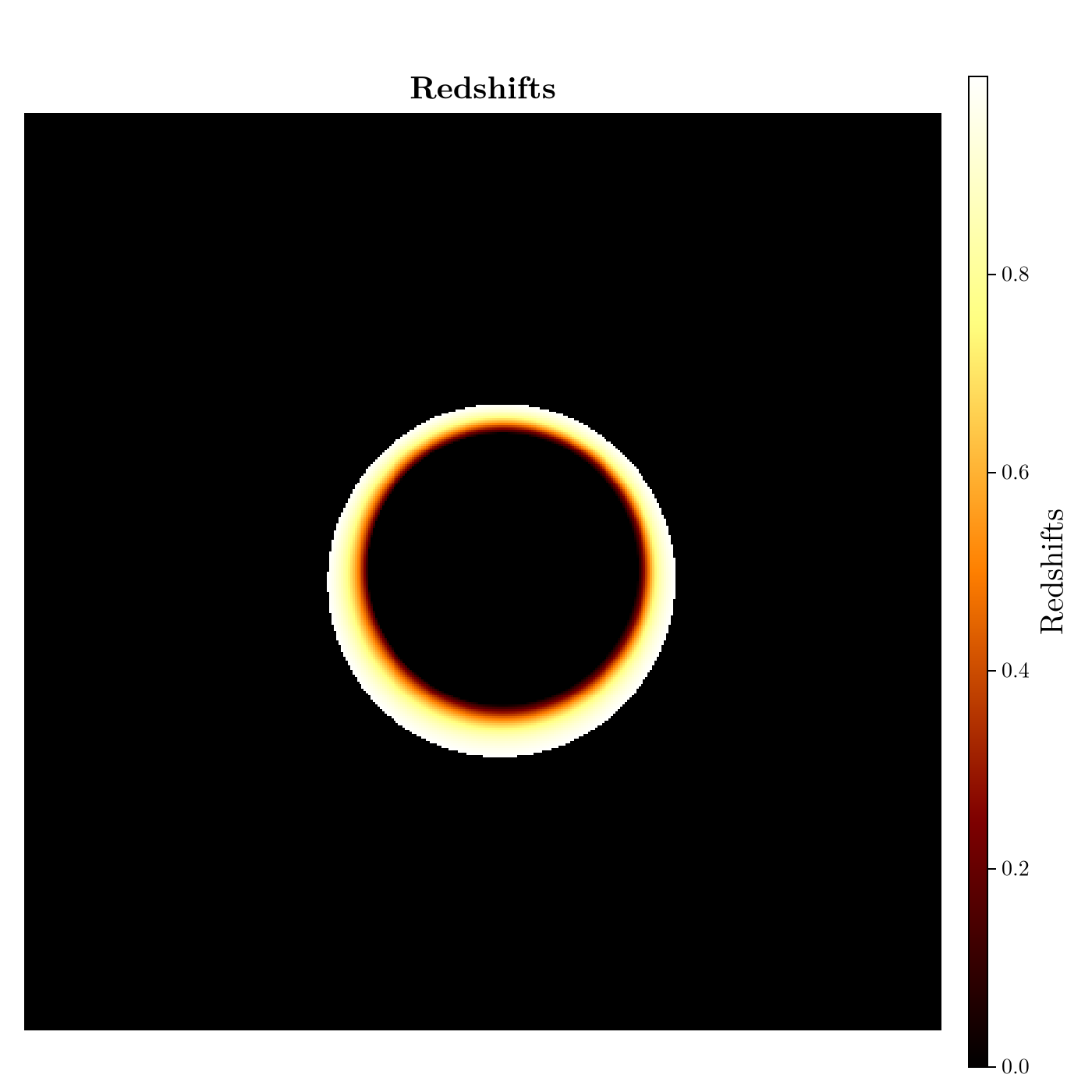

Saving the redshifts to a .npy file

using NPZ
npzwrite("redshifts_n1.npy", redshifts)

---

This page was generated using Literate.jl.