Creating a Custom Dual Cone Model

We will defined a custom model for low luminosity active galactice nuclei (LLAGN). A detailed description of the model can be found in this reference. We will show the emission of the n=0 (direct) and n=1 (indirect) photons as they are emitted from the source, at a fixed inclination angle from the blackhole's spin axis.

First, let's import Krang and CairoMakie for plotting.

using Krang
using CairoMakie

curr_theme = Theme(
    Axis = (
        xticksvisible = false,
        xticklabelsvisible = false,
        yticksvisible = false,
        yticklabelsvisible = false,
        ),
)
set_theme!(merge!(curr_theme, theme_latexfonts()))

We will use a $0.94$ spin Kerr blackhole viewed by an assymptotic observer at an inclination angle of $\theta o={17}^{\circ }$. The emission to be raytraced is

metric = Krang.Kerr(0.94);
θo = 17 * π / 180;
ρmax = 10.0;

Let's create a camera with a resolution of 400x400 pixels

camera = Krang.IntensityCamera(metric, θo, -ρmax, ρmax, -ρmax, ρmax, 400);

We will need to create Mesh objects to render the scene. First we will create the material for the mesh. Our material will be the ElectronSynchrotronPowerLawPolarization material with the following parameters.

χ = -1.705612782769303
ι = 0.5807355065517938
βv = 0.8776461626924748
σ = 0.7335172899224874
η1 = 2.6444786738735804
η2 = π-η1

0.49711397971621274

These will be used to define the magnetic field and fluid velocity.

magfield1 = Krang.SVector(sin(ι)*cos(η1), sin(ι)*sin(η1), cos(ι));
magfield2 = Krang.SVector(sin(ι)*cos(η2), sin(ι)*sin(η2), cos(ι));
vel = Krang.SVector(βv, (π/2), χ);

This material also requires the definition of a profile function. We will take a double power law in radius.

function profile(r)
    R = 3.3266154761905455
    p1 = 4.05269835622511
    p2 = 4.411852974336667
    return (r/R)^p1/(1+(r/R)^(p1+p2))
end

material = Krang.ElectronSynchrotronPowerLawPolarization();

Next we will define the geometries of each mesh. We will use a ConeGeometry with an opening angle of ${75}^{\circ }$. The additional information needed for the material will be passed as attributes to the geometry. This includes the sub-images to raytrace, which in our case will be the n=0 and n=1 sub-images.

θs = (75 * π / 180)
geometry1 = Krang.ConeGeometry((θs), (magfield1, vel, (0,1,), profile, σ))
geometry2 = Krang.ConeGeometry((π-θs), (magfield2, vel, (0,1,), profile, σ))

Krang.ConeGeometry{Float64, Tuple{StaticArraysCore.SVector{3, Float64}, StaticArraysCore.SVector{3, Float64}, Tuple{Int64, Int64}, typeof(Main.profile), Float64}}(1.832595714594046, ([0.4822331381486707, 0.2616409108851046, 0.8360593485049359], [0.8776461626924748, 1.5707963267948966, -1.705612782769303], (0, 1), Main.profile, 0.7335172899224874))

We will create two meshes, one for each geometry anc create a scene with both meshes.

mesh1 = Krang.Mesh(geometry1, material)
mesh2 = Krang.Mesh(geometry2, material)
scene = Krang.Scene((mesh1, mesh2))

(Krang.Mesh{Krang.ConeGeometry{Float64, Tuple{StaticArraysCore.SVector{3, Float64}, StaticArraysCore.SVector{3, Float64}, Tuple{Int64, Int64}, typeof(Main.profile), Float64}}, Krang.ElectronSynchrotronPowerLawPolarization}(Krang.ConeGeometry{Float64, Tuple{StaticArraysCore.SVector{3, Float64}, StaticArraysCore.SVector{3, Float64}, Tuple{Int64, Int64}, typeof(Main.profile), Float64}}(1.3089969389957472, ([-0.4822331381486707, 0.26164091088510466, 0.8360593485049359], [0.8776461626924748, 1.5707963267948966, -1.705612782769303], (0, 1), Main.profile, 0.7335172899224874)), Krang.ElectronSynchrotronPowerLawPolarization()), Krang.Mesh{Krang.ConeGeometry{Float64, Tuple{StaticArraysCore.SVector{3, Float64}, StaticArraysCore.SVector{3, Float64}, Tuple{Int64, Int64}, typeof(Main.profile), Float64}}, Krang.ElectronSynchrotronPowerLawPolarization}(Krang.ConeGeometry{Float64, Tuple{StaticArraysCore.SVector{3, Float64}, StaticArraysCore.SVector{3, Float64}, Tuple{Int64, Int64}, typeof(Main.profile), Float64}}(1.832595714594046, ([0.4822331381486707, 0.2616409108851046, 0.8360593485049359], [0.8776461626924748, 1.5707963267948966, -1.705612782769303], (0, 1), Main.profile, 0.7335172899224874)), Krang.ElectronSynchrotronPowerLawPolarization()))

Finally, we will render the scene with the camera and plot the Stokes parameters.

stokesvals = render(camera, scene)

fig = Figure(resolution=(700, 700));
ax1 = Axis(fig[1, 1], aspect=1, title="I")
ax2 = Axis(fig[1, 2], aspect=1, title="Q")
ax3 = Axis(fig[2, 1], aspect=1, title="U")
ax4 = Axis(fig[2, 2], aspect=1, title="V")
colormaps = [:afmhot, :redsblues, :redsblues, :redsblues]

zip([ax1, ax2, ax3, ax4], [getproperty.(stokesvals,:I), getproperty.(stokesvals,:Q), getproperty.(stokesvals,:U), getproperty.(stokesvals,:V)], colormaps) .|> x->heatmap!(x[1], x[2], colormap=x[3])
fig

save("polarization_example.png", fig)

┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/gG38B/src/scenes.jl:227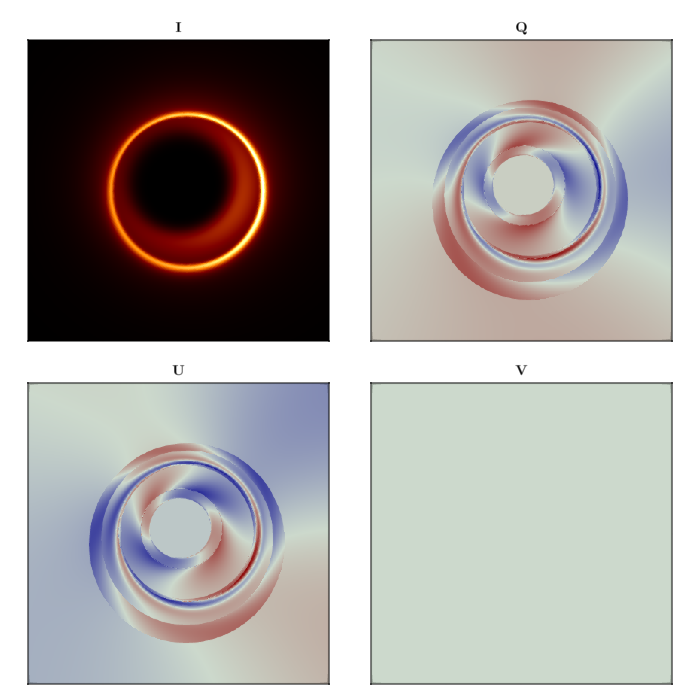

---

This page was generated using Literate.jl.