What is Krang.jl?

Kerr Raytracer for Analytic Null Geodesics (Krang) is a raytracing code for geometries that are embedded in the Kerr spacetime. Krang solves the Kerr geodesic problem using the analytic solutions that have been derived from the Hamilton-Jacobi Formalism. This choice makes the code efficient and accurate, and is an ideal formalism to isolated sub images that manifest from strong lensing.

Philosophy

The current philosophy of Krang is to raytrace meshes. Meshes are made by 'painting' materials onto geometries. These are then viewed by cameras that are sensitive to particular observables (e.g. intensity and polarization).

Meshes

Materials

Marterials define the local physics necessary to properly render geometries. Materials may sometimes need additional information that can be stored in geometries by passing attributes to the geometry constructor (see Custom Dual Cone Model for an example of passing attributes to geometries).

Geometries

There are two basic geometries currently available in Krang.

• ConeGeometry : The first is a spin axis centered cone with its apex placed at the coordinate origin.

• MeshGeometry : Geometry made from a triangular mesh. The mesh is embdedded by placing vertices at points in a Cartesian like coordinate system generated from the Boyer-Lindquist coordinates to a Cartesian like equivalent, and . There are convenience functions defines to translate, rotate and scale these geometries.

Raytracing

Light rays in this module can be parameterized in terms of either the cones (${\theta }_s$), or the minotime ($\mathrm{\Delta }\tau$). Parameterization in terms of cones allows for images to be divided into sub images and ray traced individually.

Raytracing conical surfaces

Surfaces of constant $\theta$ define spin axis centered cones whose apex lie at the origin of the Boyer-Lindquist coordinate system.

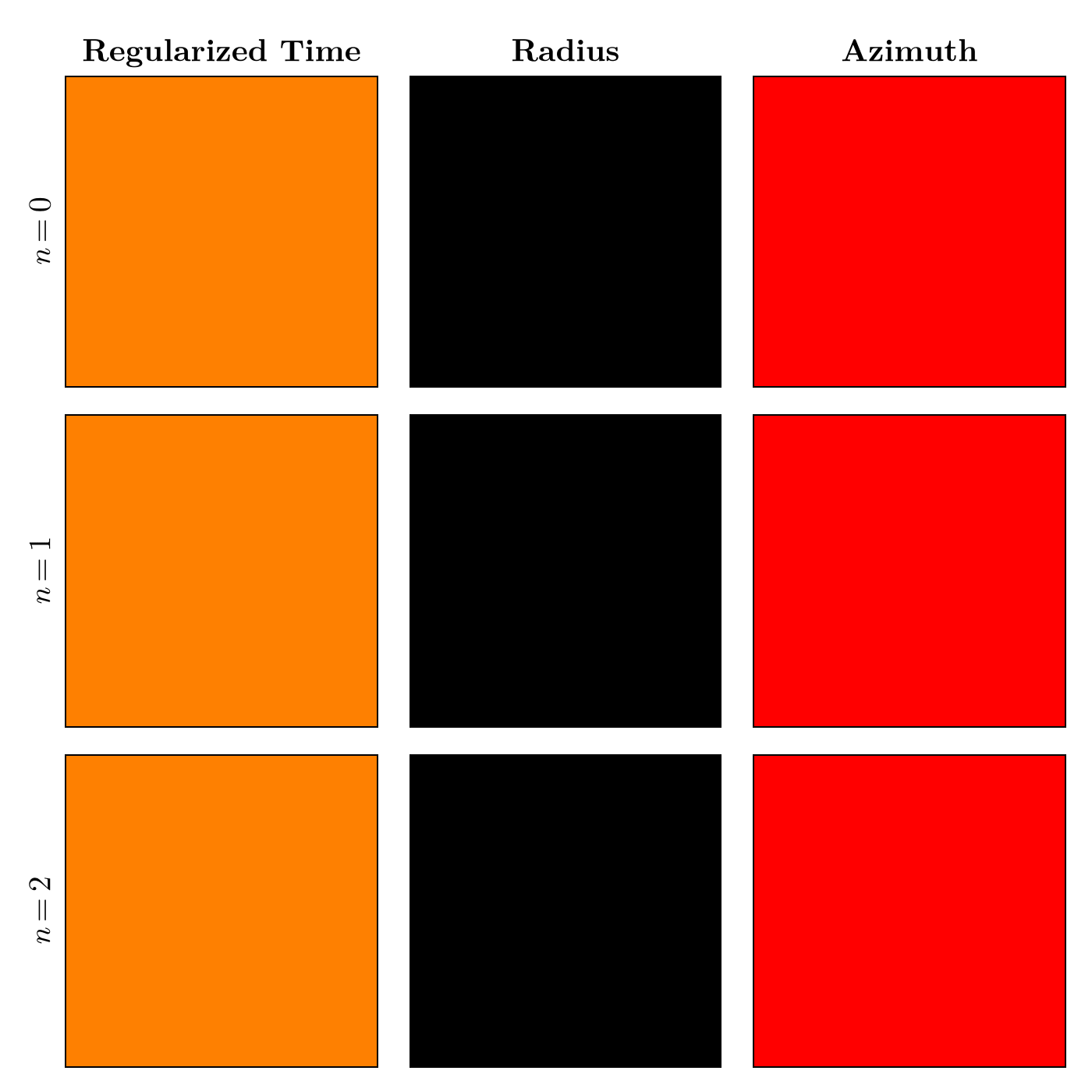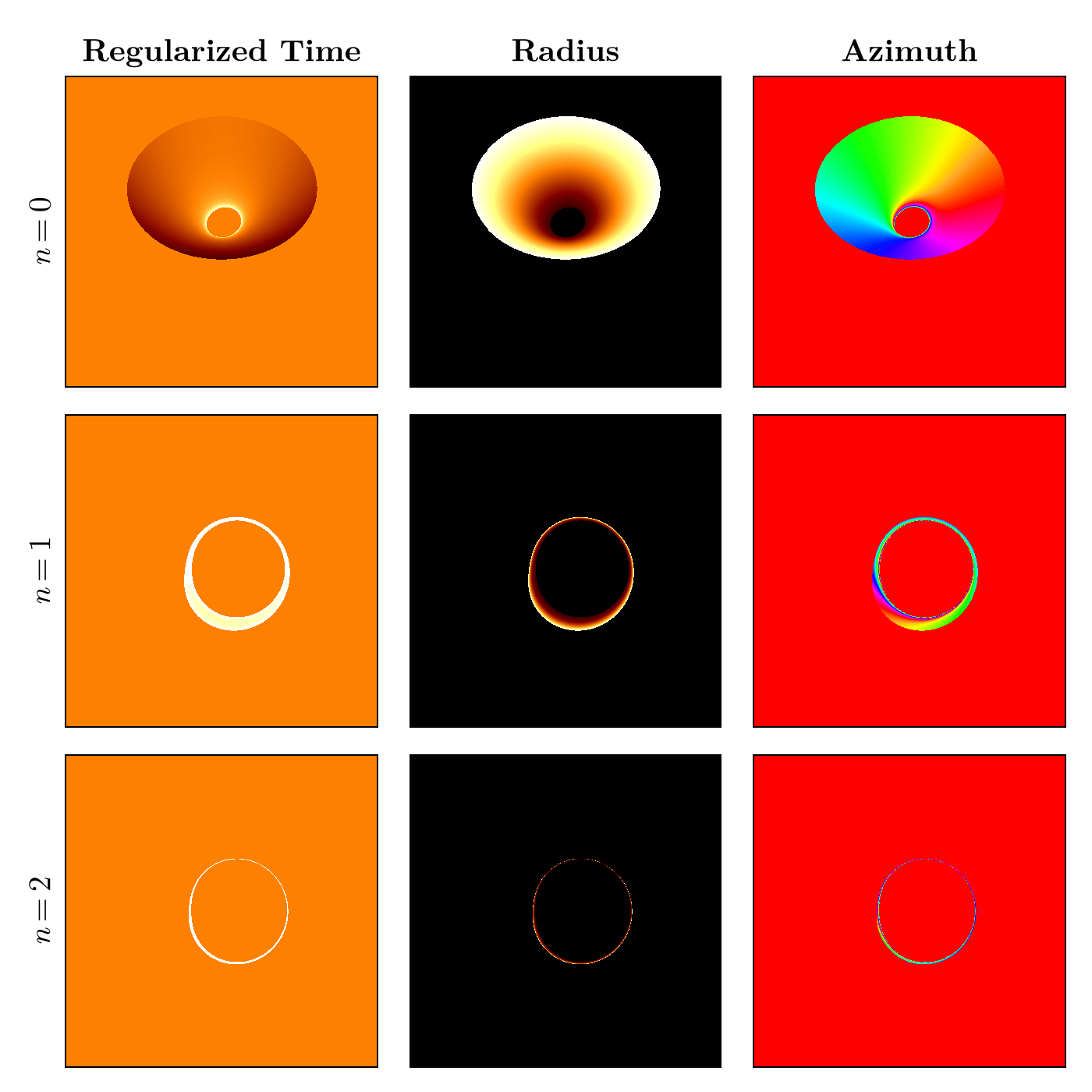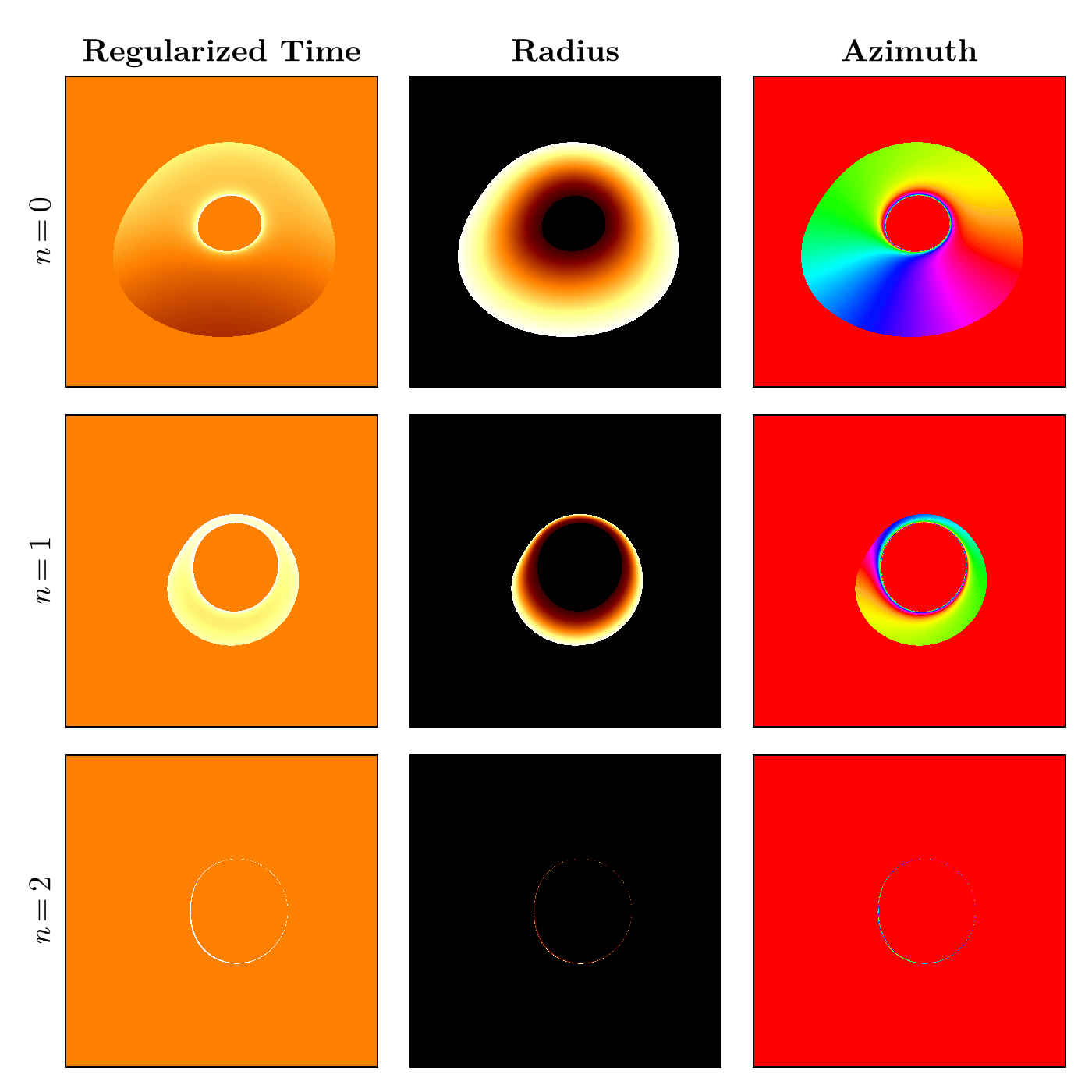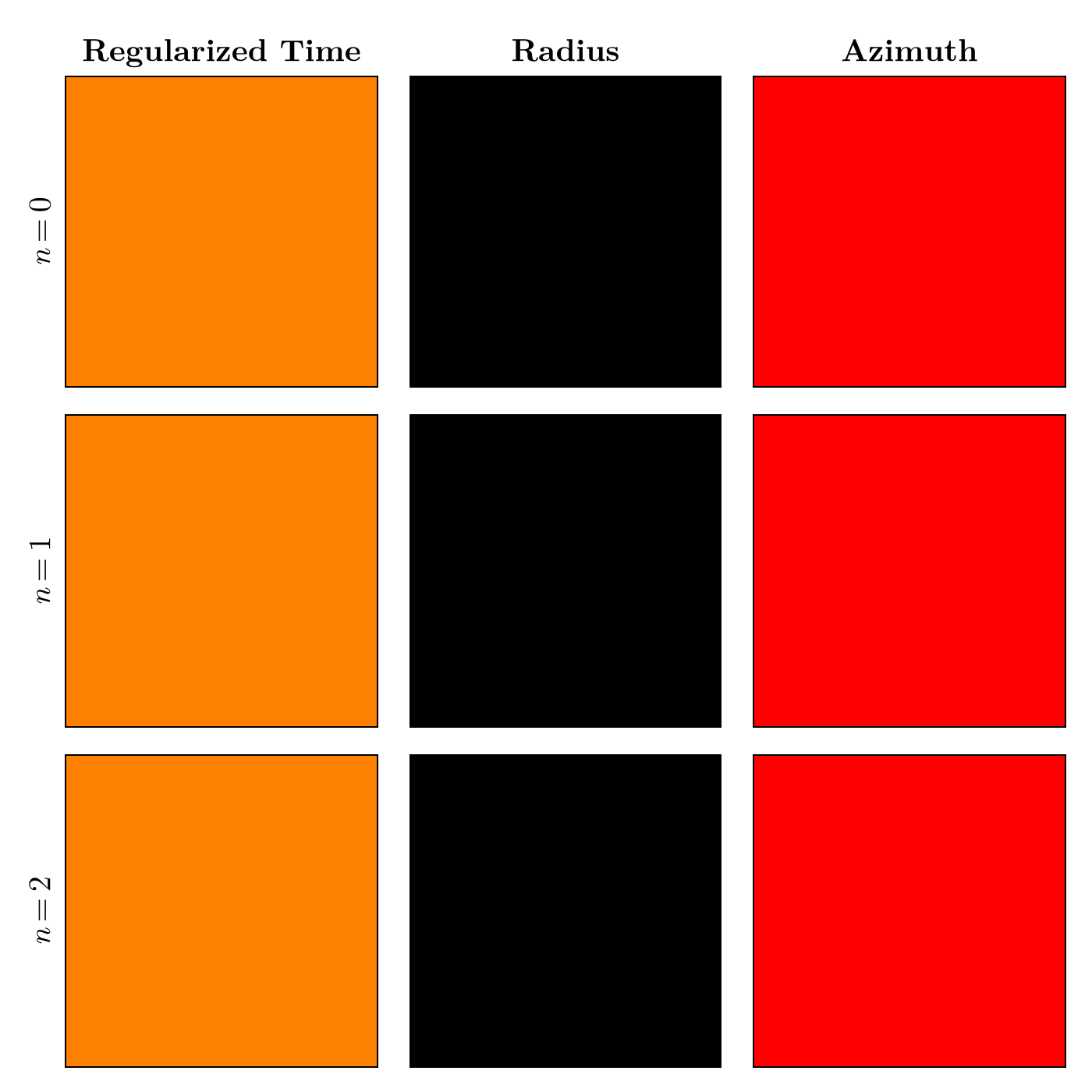
n=0 and n=1 images of emission coordinates originating from conical surfaces.

Raytracing with rays parameterized by Mino time

Mino time, 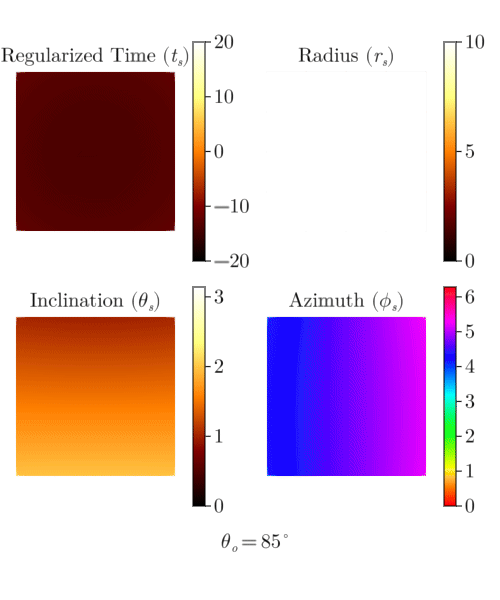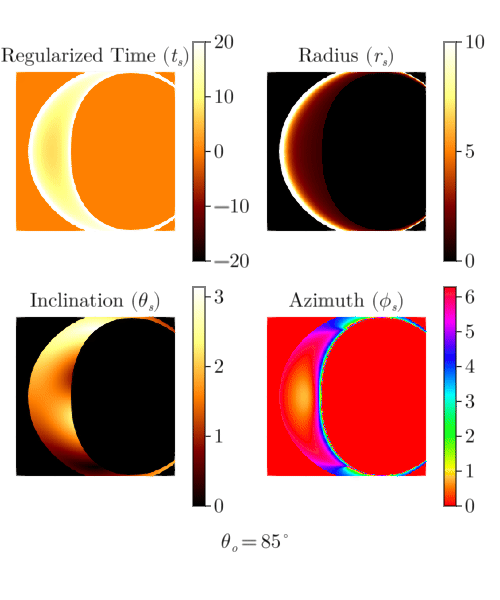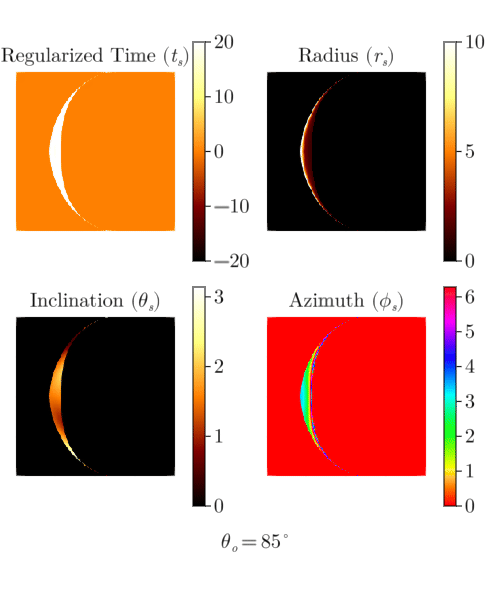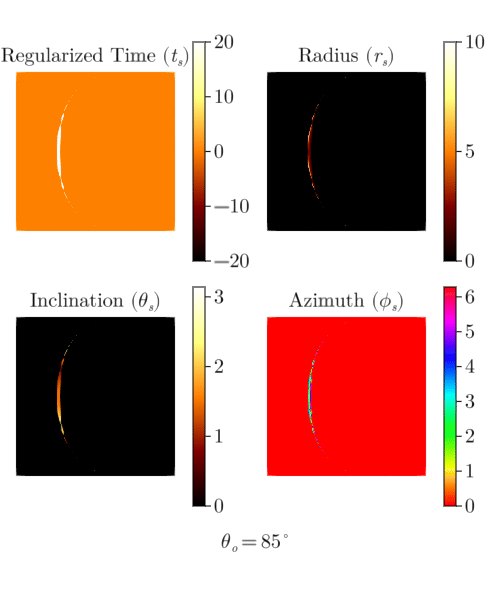$\tau$, is a parameter monotonic in affine parameter, ${\tau }^{\prime }$, defined by $ d\tau = \Sigma(r,\theta)d\tau', $ where $ \Sigma(r,\theta) = r^2 +a^2\cos^2\theta. $

Coordinate evolution with Mino time.

Cameras

Cameras store pre-computed information that is constant for a given camera location. There are currently two types of cameras which can be used for either 'slow light' or 'fast light' raytracing.

• IntensityCamera : Precomputes geodesic information necessary to solve the 'fast light' raytracing problem.

• SlowLightIntensityCamera : Precomputes geodesic information necessary to solve the 'slow light' raytracing problem.

The GPU arrays can be passed to the cameras on construction to raytrace enforce raytracing on the GPU. An sketch of how to do this with a CUDA array is:

using CUDA
 
store = CUDA.fill(0.0, sze, sze)
camera = Krang.SlowLightIntensityCamera(metric, θo, -ρmax, ρmax, -ρmax, ρmax, sze, A=CuArray)
Krang.render!(store, camera, scene)